Dear Enthusiast,
Personally, this is one of my favourite algorithm. Before we jump in to the maths and computer science part of this algorithms, first let’s understand this algorithm an analogy.
What is 0/1 Knapsack Problem Algorithm
We will first try to understand what kind of problem does it solve. We will understand with an analogy called – The Treasure Hunter's Dilemma
Imagine you are a treasure hunter on a quest to find the most valuable treasures in a limited amount of time. Your challenge is to decide which treasures to pick, considering their weights and values, while abiding by the weight capacity constraints of your treasure bag. Limited space, indicating the maximum weight your treasure chest can hold.
| Treasures | Weight | Value | 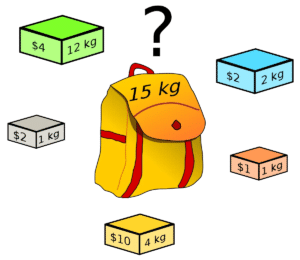 What is Knapsack’s problem |
|---|---|---|---|
| Gold coins | 5 | 4 | |
| Jewels | 6 | 3 | |
| Artifacts | 4 | 8 | |
| Rare gems | 8 | 10 | |
| Antique manuscripts | 1 | 6 | |
| Precious metals | 9 | 6 |
Objective
Now the objective is to pick up those items which are still within your treasure bag capacity maximize the total value of the treasures, where each treasure contributes to your overall wealth or value. Such problems are solved using Knapsack Algorithm.
Before solving, lets understand a bit of history about Knapsack Algorithms
History – Origin of Knapsack Problem
The term “knapsack” itself has its origins in the 17th century, derived from the German word “knapzak” which translates to “food bag.” Soldiers during that time would carry rations in a bag on their backs, facing the dilemma of selecting the most essential items without exceeding the bag’s capacity. So now you understand.. why “Knapsack” problem.
The Knapsack Problem became more formally recognized in computer science during the mid-20th century when researchers started to explore optimization problems and algorithms. Its formulation and study gained momentum as part of the broader field of combinatorial optimization.
What is the significance of 0/1 in Knapsak Problem
The term “0/1” in the context of the Knapsack Problem refers to the restriction placed on the items that can be included in the knapsack. Specifically, it means that for each item, you have a binary (0 or 1) choice — either include the entire item in the knapsack or exclude it completely. There is no option to include a fraction of an item.
This restriction distinguishes the 0/1 Knapsack Problem from the Fractional Knapsack Problem, where items can be divided and a fraction of an item can be included in the knapsack. In the 0/1 Knapsack Problem, the decision for each item is more straightforward: it’s an all-or-nothing choice.
Solving the Treasure Hunter’s 0/1 Knapsack Problem:
In Knapsack problems, there can be two types of items. They are basically dependent of types of items you are choosing. Imagine if the items are divisible like grains NOT in a packet then you can pick those items partially. In those cases, Knapsack problmes are really not useful.
1. Brute Force Approach:
Trying out all possible combinations of treasures to see which combination gives the maximum value.
However, as the number of treasures increases, this approach becomes impractical.
The time complexity of the brute-force approach to solving the Knapsack Problem is exponential, specifically O(n*2^n), where ‘n’ is the number of items. The reason for this high complexity lies in the nature of the brute-force method.
2. Greedy Approach:
The possible greedy strategies to the Knapsack problem is:
- Choose the item that has the maximum value from the remaining items; this increases the value of the knapsack as quickly as possible.
- Choose the lightest item from the remaining items which uses up capacity as slowly as possible allowing more items to be stuffed in the knapsack.
- Choose the items with as high a value per weight as possible.
This approach works well for fractional selections if partial inclusion of treasures is allowed. Ofcourse it has a better complexity than the brute force method. It is O(n*Log(n))
3. Dynamic Programming Approach:
Create a table to store intermediate results for different subproblems.
Use a recurrence relation to fill in the table and find the optimal solution efficiently.
This approach is suitable for the 0/1 Knapsack Problem, ensuring that a treasure is either included or excluded.
Let’s first make some assumption here. I am going to pass the input in the following format. It is going to be in the form of a list of tuples. Where each tuple would contain the name of the item, weight and its value. So the input array would like something like this:
[("Jewels", 2, 4) , ("Diamond", 3, 6)....]
and the second parameter would be the total capacity of the bag i.e. an Integer value.
This algorithm works something like filling this matrics to maximize the outcome of chosen items.
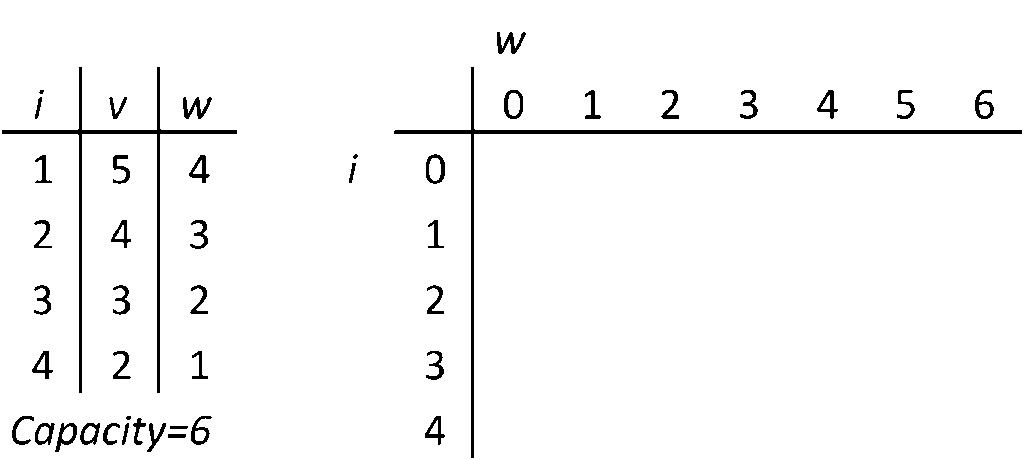
knapsack problem solving [Source wikipedia]
def knapsack_problem(items, capacity):
'''
knapsack_problem _summary_
_extended_summary_
Args:
items (_list_): List of a tuple - (Item name, weight, value)
capacity (_integer_): The maximum weight/capacity of the bag
Returns:
_tuple_: Maximum weight could be fit in the sack and list of
items which are chosen for that
'''
num_items = len(items)
# metrics with all zeros to fill all the knapsack values
knapsack_values = [[0] * (capacity + 1) for _ in range(num_items + 1)]
for i in range(1, num_items + 1):
item_name, item_weight, item_value = items[i - 1]
for c in range(capacity + 1):
if item_weight > c:
knapsack_values[i][c] = knapsack_values[i - 1][c]
else:
knapsack_values[i][c] = max(
knapsack_values[i - 1][c],
knapsack_values[i - 1][c - item_weight] + item_value,
)
max_value, selected_items = knapsack_values[num_items][capacity], []
i, c = num_items, capacity
while i > 0 and c > 0:
if knapsack_values[i][c] != knapsack_values[i - 1][c]:
selected_items.append(items[i - 1][0])
c = c - items[i - 1][1]
i = i - 1
return max_value, list(reversed(selected_items))
How to run the knapsack problem function
This is how you can pass the input parameters in the above function and get the expected result.
# Example usage:
items_list = [
("Gold coins", 5, 4),
("Jewels", 6, 3),
("Artifacts", 4, 8),
("Rare gems", 8, 10),
("Antique manuscripts", 1, 6),
("Precious metals", 9, 6)
]
knapsack_capacity = 16
result = knapsack_problem(items_list, knapsack_capacity)
print("Maximum Value:", result[0])
print("Selected Items:", result[1])

Result of knapsack problem
Real-world Applications of the Knapsack Problem:
Resource Allocation in Project Management: Optimizing the allocation of resources such as time, budget, and personnel to maximize project value.
Financial Portfolio Optimization:Selecting a combination of investments with different returns and risks to maximize the overall portfolio value.
Data Compression:Choosing a subset of files to compress within a given storage limit, optimizing for compression ratio and preserving important data.



![HEAP Data Structure – A Complete Guide [Python Code]](https://vmlogger.com/algorithms/wp-content/uploads/sites/15/2023/03/Types-of-heap-400x250.png)

0 Comments