Quick Sort: Understanding and Implementing in Python

Among the various sorting algorithms available, Quick Sort stands out as one of the efficient and widely used sorting algorithms. Although, it can offer a worst case time complexity as O(n^2) but it offers a best and an average-case time complexity of O(n log n) and performs exceptionally well in practice.
Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.[3]

In this article, we will dive into the details of the Quick Sort algorithm, understand its workings, and implement it in Python.

Introduction to Quick Sort

Similar to merge sort, quick sort is also based on divide-and-conquer algorithm principle. It was developed by British computer scientist Tony Hoare in 1959. The algorithm’s core idea is to partition the input array into two sub-arrays, where one sub-array contains elements smaller than a chosen pivot, and the other sub-array contains elements greater than the pivot.

This process is repeated recursively on the sub-arrays until the entire array is sorted. This is the reason, quick sort is also known as partition-exchange sorting algorithm.

The key steps involved in the Quick Sort algorithm are as follows:

1. Partitioning: Choose a pivot element from the array. Rearrange the array in such a way that all elements smaller than the pivot are placed before it, and all elements greater than the pivot are placed after it. The pivot element is now in its correct sorted position.
2. Recursion: Apply the partitioning step recursively to the sub-arrays formed on the left and right sides of the pivot until the entire array is sorted. This process is known as the divide-and-conquer approach.
3. Combining: Since the recursion splits the array into smaller sub-arrays, no explicit combining step is necessary. The elements are automatically combined as the recursion unwinds.

Understanding the Partitioning Process

The partitioning process plays a crucial role in Quick Sort. It determines the pivot element’s correct sorted position and rearranges the array accordingly. Several approaches exist for selecting the pivot, but the most commonly used one is the "Lomuto partition scheme."

The Lomuto partition scheme involves the following steps:

1. Choose the rightmost element of the array as the pivot.
2. Initialise a variable i to keep track of the index where elements smaller than the pivot will be placed. Initially, set i to the first element’s index, which is 0.
3. Iterate through the array from the leftmost element to the second-to-last element.
4. For each element encountered, compare it with the pivot element. If it is smaller, swap it with the element at index i and increment i by 1. This ensures that all smaller elements are placed before the pivot.
5. After the iteration completes, swap the pivot element with the element at index i. Now, the pivot element is in its final sorted position.
6. At this point, all elements to the left of the pivot (indices less than i) are smaller than the pivot, and all elements to the right of the pivot (indices greater than i) are larger than the pivot. This partitioning step ensures that the pivot element is in its correct sorted position while dividing the array into two sub-arrays for further recursion.

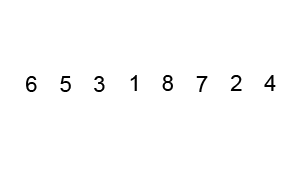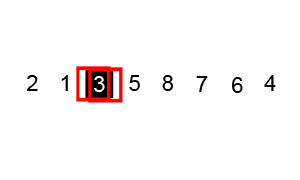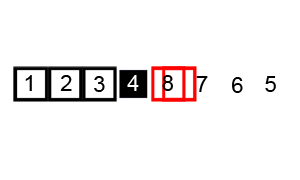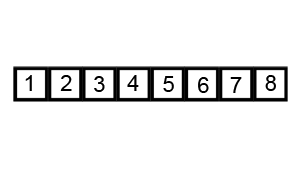
Quick Sort Animation – (Source – Wikipedia)

Implementing Quick Sort in Python – Lomuto partition scheme

Now that we have a good understanding of the Quick Sort algorithm let’s proceed to implement it in Python. Here’s the Python code for Quick Sort using the Lomuto partition scheme:

def quick_sort(arr):
    if len(arr) <= 1:
        return arr

    pivot = arr[-1]
    smaller, equal, larger = [], [], []

    for num in arr:
        if num < pivot:
            smaller.append(num)
        elif num == pivot:
            equal.append(num)
        else:
            larger.append(num)

    return quick_sort(smaller) + equal + quick_sort(larger)

Explanation about above code:

The quick_sort function takes an array arr as input and recursively performs the Quick Sort algorithm. The base case is when the array has one or fewer elements, in which case it is already sorted.

The pivot is chosen as the last element of the array (arr[-1]).
Three additional lists, smaller, equal, and larger, are initialized to store elements smaller than the pivot, elements equal to the pivot, and elements larger than the pivot, respectively.

The for loop iterates through the array, comparing each element with the pivot and appending it to the corresponding list. Finally, the function recursively calls itself on the smaller and larger lists, and combines the sorted results along with the equal list. Refer the last statement which is the return statement.

Conclusion

Quick Sort is a highly efficient sorting algorithm with an average-case time complexity of O(n log n). By cleverly choosing a pivot element and applying the divide-and-conquer approach, Quick Sort achieves fast sorting performance in practice. In this article, we explored the inner workings of the Quick Sort algorithm and implemented it in Python using the Lomuto partition scheme. Feel free to experiment with different pivot selection strategies and partitioning schemes to further enhance your understanding of this powerful sorting algorithm.